Fixed-point arithmetic is a fundamental technique in digital signal processing (DSP) and embedded systems, offering a practical alternative to floating-point operations. This arithmetic format is crucial for optimizing performance and power efficiency in FPGA (Field-Programmable Gate Array) systems. By focusing on speed and resource efficiency, fixed-point arithmetic helps enhance the performance of FPGA-based systems, making it particularly valuable in applications where floating-point precision may be excessive or where hardware resources are limited. This detailed guide will explore the basics of fixed-point arithmetic, its implementation on FPGAs, and key considerations for achieving optimal results.
Understanding Fixed-Point Numbers
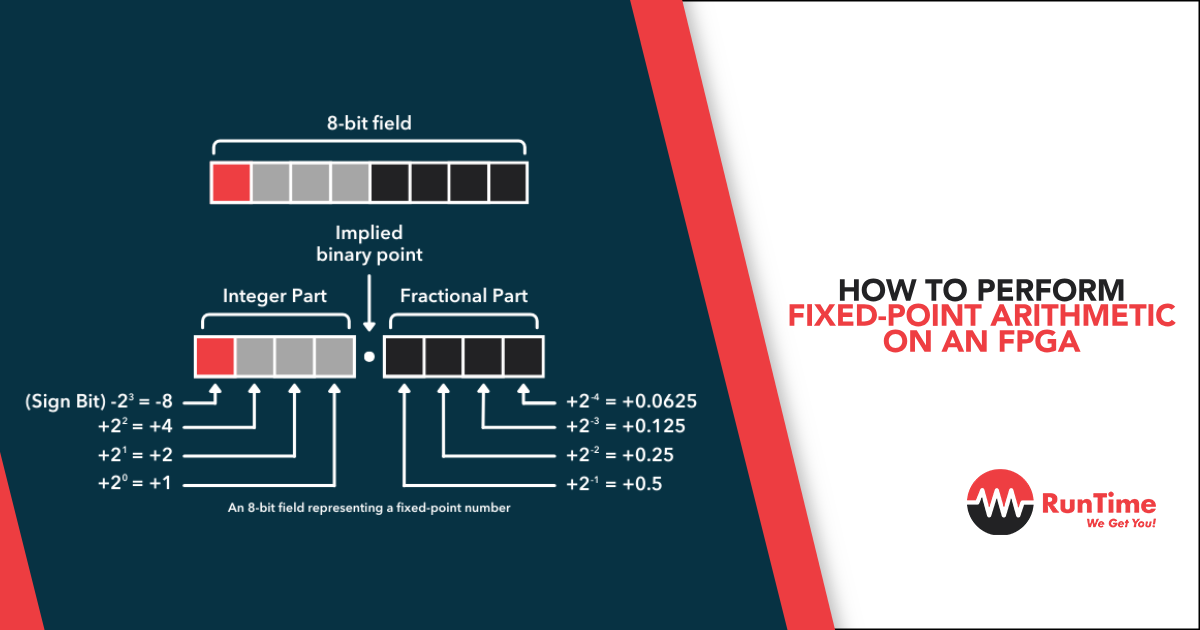
Fixed-point numbers use a fixed binary point, in contrast to floating-point numbers, which have a dynamic binary point. This fixed-point representation simplifies hardware implementation, but it requires meticulous handling of data representation, scaling, and precision.
Fixed-Point Number Representation
Fixed-point numbers are expressed in the Qm.n format:
- Q: Represents the fixed-point format.
- m: Number of integer bits.
- n: Number of fractional bits.
For instance, in a Q15.16 format, there are 15 integer bits and 16 fractional bits, making a total of 32 bits (m+n). The choice of m and n affects the range and precision of the number:
- Integer Bits (m): More integer bits increase the range of representable values. However, having too few integer bits can lead to overflow when values exceed the representable range.
- Fractional Bits (n): More fractional bits improve precision by allowing finer granularity in representing decimal values. However, too few fractional bits can cause significant precision loss.
Choosing appropriate values for m and n is essential for balancing range and precision according to the specific application requirements.
Scaling and Range
The dynamic range of a fixed-point number is determined by its total bit-width. Larger bit-widths allow for a broader range of values but require more hardware resources. Proper scaling involves adjusting the binary point position to ensure that numbers fit within the representable range and maintain the desired precision. Effective scaling ensures that the fixed-point representation aligns with the application’s needs, accommodating both the range of values and the precision required for accurate computations.
Fixed-Point Arithmetic Operations
Fixed-point arithmetic includes several fundamental operations: addition, subtraction, multiplication, and division. Each operation has unique considerations when implemented on FPGA hardware.
Addition and Subtraction
Addition and subtraction of fixed-point numbers with the same format are relatively straightforward because the binary point positions are aligned, and the operations are similar to integer arithmetic. However, when dealing with numbers of different formats, alignment is required. This involves adjusting the binary point position of one or both numbers before performing the operation to ensure that the results are accurate and meaningful.
Multiplication
Multiplying two fixed-point numbers results in a format of Q(m1+m2).(n1+n2). For example, multiplying two Q15.16 numbers yields a Q30.32 result. The resulting product may require truncation or rounding to fit into the desired output format. This operation is more complex due to the increased bit-width of the product, which can impact precision. Proper handling of the multiplication process is essential to maintain accuracy and prevent overflow.
Division
Division of fixed-point numbers is more complex compared to other arithmetic operations. It often requires iterative algorithms or dedicated hardware dividers. The format of the result depends on the formats of the dividend and divisor, as well as the precision requirements. Specialized hardware dividers optimized for fixed-point arithmetic can significantly improve speed and efficiency, making them essential for applications requiring high-performance computations.
Implementing Fixed-Point Arithmetic on FPGAs
FPGAs provide a flexible platform for implementing fixed-point arithmetic. Key considerations include hardware accelerators, custom logic, and high-level synthesis (HLS).
Hardware Accelerators
Many FPGA vendors offer dedicated hardware multipliers and dividers optimized for fixed-point operations. These accelerators enhance performance and resource efficiency by providing hardware solutions tailored to fixed-point arithmetic.
- Multipliers: FPGA-specific multipliers are designed to handle fixed-point multiplication with high efficiency. They support high-throughput operations and can handle the increased bit-width required for accurate multiplication. By using dedicated multipliers, engineers can significantly reduce computation time and improve overall performance.
- Dividers: Hardware dividers perform fixed-point division with minimal latency. These dividers are optimized for fixed-point operations, enhancing computational speed and reducing the time required for division. Efficient division operations are crucial for high-performance applications, and hardware dividers play a significant role in achieving this efficiency.
Utilizing these hardware accelerators can greatly improve the efficiency of fixed-point operations on FPGAs, leveraging the hardware resources effectively to achieve faster and more reliable arithmetic operations.
Custom Logic
Custom logic design using FPGA fabric allows for the creation of specialized arithmetic operations tailored to specific application needs. This approach offers maximum flexibility but requires careful optimization to ensure efficient performance.
- Designing Custom Logic: Engineers can design custom arithmetic units using FPGA primitives such as look-up tables (LUTs) and flip-flops. This customization allows for tailored solutions that meet specific performance and resource requirements. Designing custom logic involves creating arithmetic units that fit the exact needs of the application, which can enhance both performance and efficiency.
- Optimization: Techniques such as pipelining, parallelism, and resource sharing are essential for optimizing custom logic. Pipelining involves breaking down operations into stages to increase throughput, while parallelism allows for the simultaneous execution of multiple operations. Resource sharing helps manage hardware resources efficiently, reducing redundancy and improving overall performance. These optimization techniques are crucial for achieving high-performance fixed-point arithmetic on FPGA.
- Testing and Verification: Thorough testing and verification are vital for ensuring the correctness and performance of custom logic. Simulation tools and hardware emulation are essential for validating designs before hardware implementation. These tools help identify and address potential issues, ensuring that the custom logic operates correctly and efficiently in the FPGA environment.
High-Level Synthesis (HLS)
High-Level Synthesis (HLS) tools convert high-level C or C++ code into hardware descriptions, simplifying the design process. HLS tools abstract hardware design details, enabling engineers to focus on high-level functionality and algorithmic development.
- HLS Workflow: Engineers write code in high-level languages, and HLS tools generate hardware descriptions (e.g., VHDL or Verilog) from this code. This process allows for the rapid development of hardware designs, reducing the need for manual coding and enabling engineers to explore design alternatives more efficiently.
- Advantages: HLS tools streamline the design process by automating the conversion of high-level code into hardware descriptions. They support optimizations such as loop unrolling and pipelining, which can enhance performance and efficiency. By reducing manual coding efforts, HLS tools accelerate development cycles and facilitate the exploration of design options.
- Considerations: Although HLS tools simplify the design process, the generated hardware must meet performance and resource requirements. Engineers may need to perform tuning and optimization to ensure that the final implementation adheres to specific constraints and performs efficiently. Careful analysis and adjustment are necessary to achieve optimal results with HLS tools.
Challenges and Solutions in Fixed-Point Arithmetic
Implementing fixed-point arithmetic presents several challenges that must be addressed to ensure accurate and efficient results. Key challenges include overflow, underflow, and quantization error.
Overflow and Underflow
- Overflow: Overflow occurs when the result of an operation exceeds the representable range of the fixed-point format. To manage overflow, techniques such as saturation arithmetic (clamping results to maximum or minimum values) and modular arithmetic (result wrapping around) can be employed. Saturation arithmetic prevents results from exceeding the representable range by clamping them to the maximum or minimum values, while modular arithmetic allows results to wrap around, ensuring that they remain within the representable range.
- Underflow: Underflow occurs when the result is smaller than the smallest representable value. Proper format selection and scaling are essential for mitigating underflow. Analyzing data ranges and scaling factors helps ensure that the fixed-point representation can accommodate the expected range of values, preventing underflow issues.
Quantization Error
Quantization error arises from converting floating-point numbers to fixed-point representations or truncating results. This error affects computation accuracy and requires careful analysis to manage effectively.
- Error Analysis: Performing quantization error analysis helps understand the impact of fixed-point representation on computation accuracy. Effective error budgeting involves evaluating the trade-offs between precision and resource usage, ensuring that the fixed-point implementation meets the required accuracy. Techniques such as rounding and truncation can be employed to manage quantization error and maintain desired precision levels.
- Error Mitigation: Strategies for mitigating quantization error include selecting an appropriate fixed-point format, using error analysis tools, and adjusting scaling factors. Proper design and optimization help minimize error and ensure that the fixed-point arithmetic implementation meets the required precision and accuracy.
Fixed-Point Design Flow
A systematic design flow is crucial for successful fixed-point implementation. The design flow typically includes the following steps:
- Algorithm Analysis and Data Range Determination: Analyze the algorithm to determine data range requirements. Understanding the characteristics of the input data and the required precision helps in selecting an appropriate fixed-point format. This step involves evaluating the algorithm’s requirements and ensuring that the fixed-point representation aligns with the application’s needs.
- Fixed-Point Format Selection: Choose a fixed-point format based on data range and precision needs. Selecting the number of integer and fractional bits involves balancing the trade-offs between range and precision to meet the application’s requirements. This step is critical for ensuring that the fixed-point representation is suitable for the specific use case.
- Simulation and Verification: Simulate the fixed-point implementation to verify correctness and performance. This step includes validating the design against expected behavior, ensuring that it operates within specified constraints, and identifying any potential issues. Simulation and verification help ensure that the fixed-point arithmetic implementation performs correctly and meets the required specifications.
- Hardware Implementation and Optimization: Implement the design on FPGA and optimize for performance and resource usage. Techniques such as pipelining, parallel processing, and efficient resource management are essential for achieving optimal performance and resource utilization. This step involves translating the fixed-point design into hardware and optimizing it to meet performance and resource constraints.
- Testing and Validation: Conduct thorough testing and validation of the hardware implementation to ensure that it meets the required specifications and performs as expected. This includes functional testing, performance evaluation, and reliability assessment. Comprehensive testing and validation help confirm that the fixed-point arithmetic implementation operates correctly and efficiently in the FPGA environment.
Conclusion
Fixed-point arithmetic is a powerful tool for FPGA-based systems, offering significant benefits in terms of performance and power efficiency. By understanding the principles of fixed-point representation and operations, and leveraging FPGA resources effectively, engineers can develop optimized solutions for a wide range of applications. Addressing challenges such as overflow, underflow, and quantization error, and following a systematic design flow, ensures successful fixed-point arithmetic implementation on FPGAs. Through careful design, analysis, and optimization, engineers can achieve high-performance and reliable fixed-point arithmetic solutions for their applications.
Hire the Best Engineers with RunTime
At RunTime, we are dedicated to helping you find the best Engineering talent for your recruitment needs. Our team consists of engineers-turned-recruiters with an extensive network and a focus on quality. By partnering with us, you will have access to great engineering talent that drives innovation and excellence in your projects.
Discover how RunTime has helped 423+ tech companies find highly qualified and talented engineers to enhance their team’s capabilities and achieve strategic goals.
On the other hand, if you’re a control systems engineer looking for new opportunities, RunTime Recruitment’s job site is the perfect place to find job vacancies.